순열
순열(permutation)은 순서가 정해진 임의의 집합을 다른 순서로 섞는 연산을 뜻한다. 가령 {1,2,3}이라는 집합에서 순서를 고려하여 3가지 숫자를 뽑는경우는 {1,2,3], {1,3,2},{2,1,3},{2,3,1},{3,1,2},{3,2,1} 6가지 경우의 수가 나오게되고 이처럼 특정 집합의 요소들을 순서를 고려하여 뽑는 경우를 순열이라고 한다.
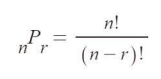
n개의 집합에서 r개의 요소를 뽑는 경우를 nPr이라고 하고 공식은 위와 같다.
구현
1. 내장 함수 기반 구현
c++은 내부적으로 순열을 구현해주는 next_permutation()함수를 가지고 있다. (algorithm 헤더안에 포함)

인자값으로 범위를 넣어주면 되는데 [fisrt, last) 범위로 값을 넣어주면된다.
따라서 (1,2,3) : i = 0 ~ 2 의경우 0 ~ 3(마지막 + 1)을 넣어줘야 0 ~ 2까지의 인덱스가 정상적으로 출력
#include <iostream>
#include <algorithm>
using namespace std;
int main() {
int arr[] = { 1,2,3 };
do {
for (int v : arr)
cout << v << " ";
cout << "\n";
} while (next_permutation(arr, arr + 3));
return 0;
}

만약 배열이 아닌 벡터를 사용하게되면 next_permutaion(vector.begin(), vector.end())를 넣어주면 된다. (vector.end()는 마지막 배열 + 1번쨰를 리턴하므로)
next_permutation 사용시 순열을 뽑아서 새로운 배열을 만드는것이 아닌 기존의 배열의 순서 구성 자체 바꾸는것임을 기억하자.
주의사항
next_permutation은 오름차순으로 정렬된 배열 기반으로 정렬을 수행해야하는데 이는 next_permutation()함수가 현재 배열의 다음 번쨰 순열을 만드는것이기 떄문이다.
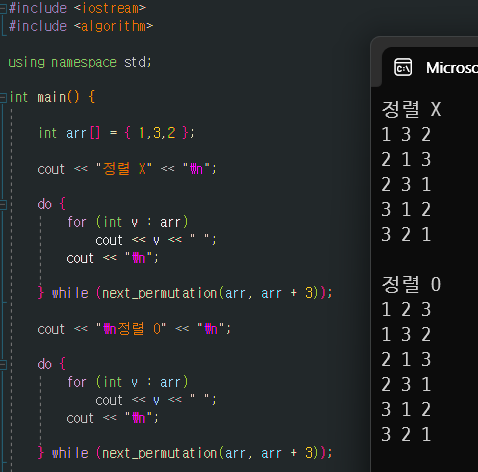
정렬이 되지 않은 배열의 순열을 구할경우 모든 순열을 구하지 못하는것을 볼 수 있는데 정렬 되지 않은 (1,3,2)라는 배열로 시작하게되면 (1,3,2) 다음순열은 (2,1,3) -> (2,3,1) ... 이므로 (1,3,2) 보다 앞선 경우의 순열 조합은 구하지 못하게된다. 따라서 반드시 정렬을 수행하고 순열 탐색을 시작해야한다.
2. 재귀 기반 순열
#include <iostream>
#include <algorithm>
using namespace std;
int arr[] = { 1,2,3 };
int n = 3, r = 3;
void makePermutation(int n, int r, int depth) {
if (depth == r) { // r개를 모두 뽑은 경우 출력하고 리턴
for (int i = 0; i < r; i++)
cout << arr[i] << " ";
cout << "\n";
return;
}
for (int i = depth; i < n; i++) {
swap(arr[i], arr[depth]);
makePermutation(n, r, depth + 1);
swap(arr[i], arr[depth]);
}
return;
}
int main() {
makePermutation(n, r, 0);
return 0;
}
1.depth 번쨰 배열을 i번째 배열과 교체
2.makePermutation() 재귀 이떄 depth + 1 (depth번째 요소는 이미 뽑앗기에 고정해두고 그 다음 요소의 위치를 정해야 하므로 depth + 1)
3. 기저사례를 만나 재귀가 종료된경우 이전 배열 상태로 되돌려준다 (그래야 모든 경우의 수를 탐색 가능)

조합
조합(combination)은 순열과 달리 순서를 신경쓰지않고 임의의 집합에서 r개를 뽑는 연산이다. 가령 {1,2,3, 4}이라는 집합에서 순서를 고려하지 않고 3가지 숫자를 뽑는경우는 {1,2,3], {1,2,4}, {1,3,4}, {2,3,4} 4가지 경우의 수가 나오게되고 이처럼 특정 집합의 요소들을 순서를 고려하지 않고 뽑는 경우를 조합이라고 한다.
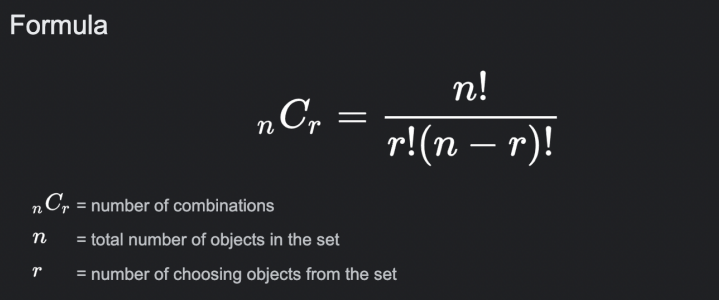
n개의 집합에서 순서를 고려 하지 않고 r개의 요소를 뽑는 경우를 nCr이라고 하고 공식은 위와 같다.
구현
'알고리즘 공부' 카테고리의 다른 글
| 유클리드 호제법 (0) | 2023.07.25 |
|---|---|
| 해시맵 (feat.백준 7785번) (0) | 2023.06.23 |
| 이진 탐색 (feat. 백준14425번) (0) | 2023.06.21 |
| 힙정렬 (0) | 2023.06.12 |
| Floyd Warshall 알고리즘 (0) | 2023.06.12 |
