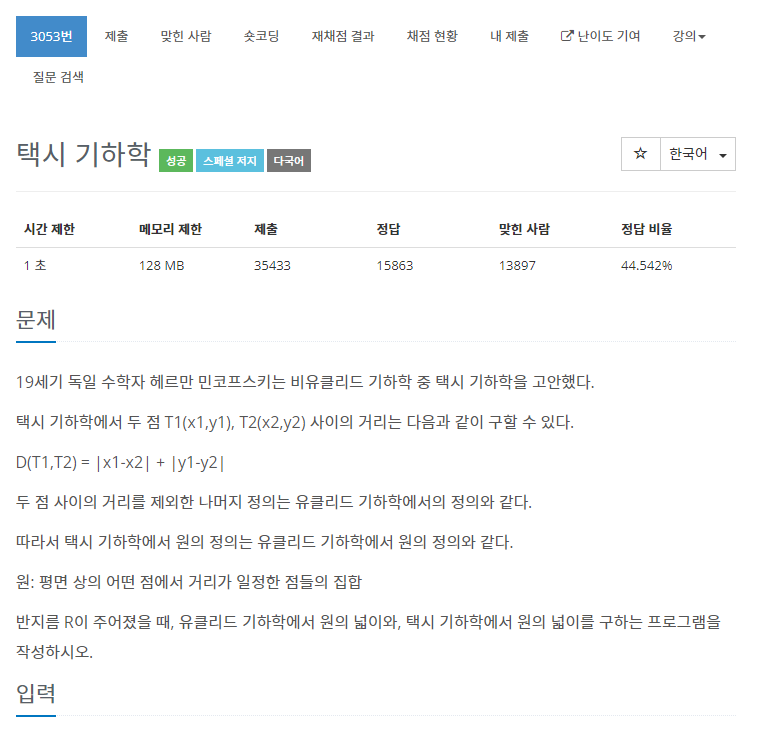
1.문제
2.풀이
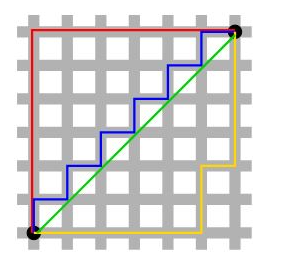
우리가 흔히 하는 유클리드 기하학에서 원이라 함은 한점에서부터 다른한점까지의 거리가 모두 일정한 선들의 집합을 뜻한다. 여기서 한점과 다른 한 점 사이의 거리는 다음과같다.

즉 첫번째 사진의 초록색 선을 유클리드기하학에서 구한 두점사이의 거리이다.
택시기하학의 경우 이동한 거리를 두 점 사이의 거리로 정의한다(빨간색 선). 그래서 택시 기하학에서의 거리는 다음과 같이 정의 할 수 있다.
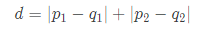
그래서 만약 택시 기하학에서 반지름이 2인 원을 그리고자 하면 이동거리가 2가되는 모든 점들을 찍어보면 된다.

그래서 택시기하학의 원은 마름모 형태가 나온다.
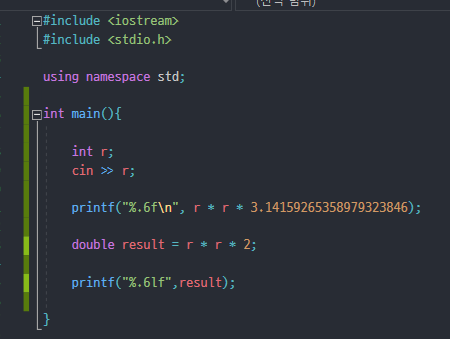
원의 넓이와 마름모의 넓이를 구하면 답을 구할 수 있다.
이때 float을 사용하면 정확도가 낮아 틀렸지만 같은 코드를 double로 바꿔서 제출하니 정답을 받았다.
1.문제

2.풀이

우리가 흔히 하는 유클리드 기하학에서 원이라 함은 한점에서부터 다른한점까지의 거리가 모두 일정한 선들의 집합을 뜻한다. 여기서 한점과 다른 한 점 사이의 거리는 다음과같다.

즉 첫번째 사진의 초록색 선을 유클리드기하학에서 구한 두점사이의 거리이다.
택시기하학의 경우 이동한 거리를 두 점 사이의 거리로 정의한다(빨간색 선). 그래서 택시 기하학에서의 거리는 다음과 같이 정의 할 수 있다.
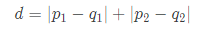
그래서 만약 택시 기하학에서 반지름이 2인 원을 그리고자 하면 이동거리가 2가되는 모든 점들을 찍어보면 된다.

그래서 택시기하학의 원은 마름모 형태가 나온다.

원의 넓이와 마름모의 넓이를 구하면 답을 구할 수 있다.
이때 float을 사용하면 정확도가 낮아 틀렸지만 같은 코드를 double로 바꿔서 제출하니 정답을 받았다.
