개요
Floyd Warshall 알고리즘은 Dijkstra 알고리즘과 마찬가지로 그래프에서 정점간의 최단경로를 찾기 위한 대표적인 최단경로 알고리즘중 하나이다.
비슷한 알고리즘이지만 Dijkstra는 한 특정 지점에서 다른 모든 지점까지의 최단경로를 구하는 Single-source shortest path algorithm이고, Floyd Warshall의 경우 모든 지점에 대해 그 점을 제외한 다른 지점들 까지의 모든 최단경로를 구하는 All-pairs shortest path algorithm이라는 차이점이 있다.
이번 글에서는 모든 쌍에 대해 최단 경로를 구하는 Floyd Warshall알고리즘에 대해 알아보고자 한다.
아이디어
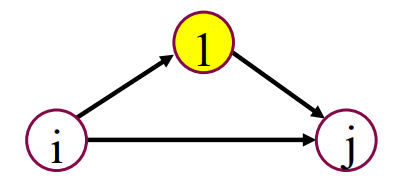
위 사진처럼 i, j, 1 이라는 3개의 노드가 연결된 그래프가 있다고 가정하자.
이 경우 i -> j 로 가기 위한 경로는 다음과 같다
- i 에서 바로 j로 가는 경우 (i -> j)
- i 에서 1을 경유한뒤 j로 가는 경우 (i -> 1 -> j)
이 두가지 경우를 비교하여 더 짧은 경로를 선택한다면 i에서 j로 가기위한 최단 경로를 선택하는 셈이 된다.
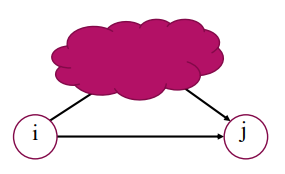
하지만 실제 그래프의경우 이처럼 단순한 구조가 아니고 여러 노드들이 연결되어있다. 따라서 i 에서 j가는 경우를 하나의 부분문제로 생각하고 이를 반복해나가면서 최종적인 해를 얻는 DP방식을 활용한다.
즉, 경유가능한 선택지 노드를 1,2,3 ... n까지 고려하면서 단계적으로 최단경로를 찾는다.
풀이
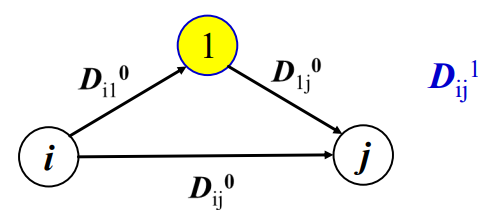
1을 경유하여 i에서 j까지 가는 최단경로를 D(ij1)이라고 가정한다면
D(ij1) = min(D(i,j,0), D(i,1,0) + D(1,j,0))이 된다.
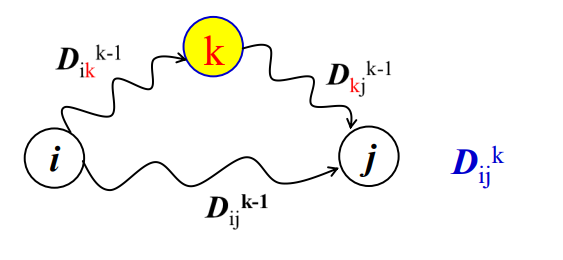
따라서 식을 세워보면 k를 경유해서 i부터 j까지 가는 경우는 D(ijk) = min(D(i,j,k), D(i,k,k-1) + D(k,j,k-1))이 된다.
따라서 모든 k의 경우의 수를 반복하면 i부터 j까지가는 최단 경로를 구할수 있게 된다.

DP 점화식 : D[i,j] = min(D[i,j], D[i,k] + D[k,j])
코드(C++)
#include <iostream>
#include <string>
#include <vector>
using namespace std;
#define N 10
int INF = 1000000;
int route[N][N] = { // 그래프 간선 연결
{0,12,15,INF,INF,INF,INF,INF,INF,INF},
{12,0,INF,INF,4,10,INF,INF,INF,INF},
{15,INF,0,21,INF,INF,7,INF,INF,INF,},
{INF,INF,21,0,INF,INF,INF,25,INF,INF},
{INF,4,INF,INF,0,3,INF,INF,INF,INF},
{INF,10,INF,INF,3,0,10,INF,INF,INF},
{INF,INF,7,INF,INF,10,0,19,INF,9},
{INF,INF,INF,25,INF,INF,19,0,INF,5},
{INF,INF,INF,INF,13,INF,INF,INF,0,15},
{INF,INF,INF,INF,INF,INF,9,5,15,0},
};
int result[N][N];
bool visited[N]; // 방문한 노드 체크 하기 위한 배열
void FloydWarshall()
{
for (int k = 0; k < N; k++) {
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
int temp = route[i][k] + route[k][j];
if (temp < route[i][j])
route[i][j] = temp;
}
}
}
}
void printTable(bool isDijkstra) // FloydWarshall 결과 출력
{
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
cout << route[i][j] << " ";
}
cout << endl;
}
cout << endl;
}
int main() {
FloydWarshall();
cout << "========== FloydWarshall 실행 결과 ==========" << endl << endl;
printTable(false);
return 0;
}'알고리즘 공부' 카테고리의 다른 글
| 조합과 순열 (0) | 2024.01.13 |
|---|---|
| 유클리드 호제법 (0) | 2023.07.25 |
| 해시맵 (feat.백준 7785번) (0) | 2023.06.23 |
| 이진 탐색 (feat. 백준14425번) (0) | 2023.06.21 |
| 힙정렬 (0) | 2023.06.12 |
